深度学习基础 - MNIST实验（tensorflow+MLP）

发表于 | 分类于 | | 阅读次数:

采用MLP（多层感知机）模型进行mnist分类任务，尝试Adam、Dropout等训练策略。

本文的完整代码托管在我的Github PnYuan - Practice-of-Machine-Learning - MNIST_tensorflow_demo，欢迎交流。

1.任务背景

在前一篇深度学习基础 - MNIST实验（tensorflow+Softmax）的基础上，我们进一步引入MLP（multi-layer perceptron - 多层感知机）来进行mnist实验，以期实现更好的识别效果。

关于mnist数据集的相关基础信息可参考前一篇文章或MNIST官网。

2.实验过程

实验参考代码：python + tensorflow

2.1.MLP建模

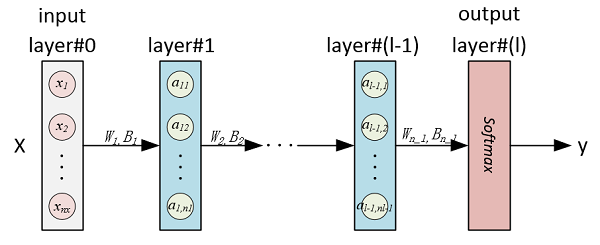
这里，MLP用于MNIST分类实验，输入是x - 28×28=784的图片灰度向量，输出是类别标签y ~ [0,1,2,...,9]，拟构建的MLP（全连接NN）模型如下图示：

mlp_graph

这里我们从一个无隐含层模型（即Softmax）开始，逐渐增加神经网络规模，来观察效果变化情况。

为适应任意层数和层内神经元节点数的开发需求，编写参数初始化和前向传播函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
'''(MLP) parameter initial'''
def mlp_param_init(dim):
    """
    @note: Initializes parameters to build a multi-layer perceptron with tensorflow.
        The shapes are:
            W1: [n1, n_x]
            B1: [n1, 1]
            W2: [n2, n1]
            B2: [n2, 1]
            ...
            Wl: [n_y, nl-1]
            Bl: [n_y, 1]
        
    @param dim: the number of unit in each level -- dim = [n_x, n1, n2, ..., n(l-1), n_y]    
    @return: parameters -- a dictionary of tensors containing W1, b1, W2, b2, W3, b3
    """
    parameters = {}
    l = len(dim)  # the layers' count
    
    # parameter initializing (using xavier_initializer for weight) (from 0 - input to l-1 - output)
    for i in range(1, l):
        parameters['W'+str(i)] = tf.get_variable('W'+str(i), [dim[i], dim[i-1]], initializer = tf.contrib.layers.xavier_initializer())   
        parameters['B'+str(i)] = tf.get_variable('B'+str(i), [dim[i], 1], initializer = tf.zeros_initializer())

    return parameters

'''(MLP) forward propagation'''
def mlp_forward_propagation(X, parameters):
    """
    @note: Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU ... -> LINEAR -> (SOFTMAX)
    
    @param X: input dataset placeholder, of shape (input size, number of examples)
    @param parameters: python dictionary containing your parameters "W1", "B1", "W2", "B2", ... the shapes are given in initialize_parameters.
                       
    @return: Z_l the output of the last LINEAR unit
    """
        
    l = int(len(parameters)/2)  # the number of layer
    
    # for hidden layer(linear-->relu)
    A = X
    for i in range(1, l):
        W = parameters['W'+str(i)]
        B = parameters['B'+str(i)]
        Z = tf.add(tf.matmul(W, A), B)  # Z = np.dot(W, X) + B
        A = tf.nn.relu(Z)               # A = relu(Z)
    
    # for output layer(linear-->softmax) softmax is canceled here
    W = parameters['W'+str(l)]
    B = parameters['B'+str(l)]
    Z_l = tf.add(tf.matmul(W, A), B)

    return Z_l

这样，通过输入神经网络维度变量dim，可构建出相应的MLP计算图。

2.2.训练与测试

设置超参数（如learning rate=0.05、mini-batch size=128、optimizer=GD等），加载MNIST数据集，然后通过在Session下运行Optimizer来进行训练。得出不同神经网络规模下效果如下，这里的模型效果由分类准确率（Accuracy）来衡量。

dim NN层数 参数规模 训练时耗 Accuracy （Train/Valid/Test）
[784,10] 1 7850 1’38” 90.5% / 91.0% / 91.0%
[784,20,10] 2 15910 1’34” 92.6% / 92.9% / 92.7%
[784,30,100,30,10] 4 29990 1’57” 95.3% / 95.4% / 95.0%

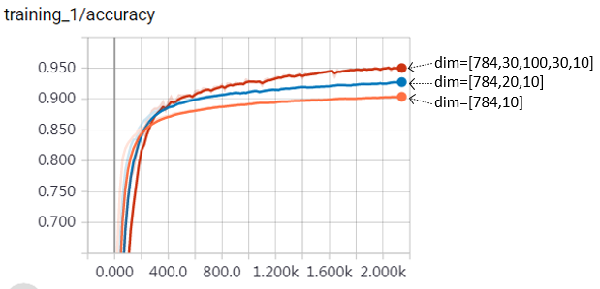
对比上表三次训练可看出，随着神经网络规模的扩大，模型效果越来越好。截取tensorboard监视器上关于accuracy指标的变化曲线，进一步可对比如下图：

acc_compare_size

2.3.改进

2.3.1.优化策略-Adam

采用Momentum、Adam等优化策略替代原始的Gradient Descent，可以促进优化收敛，下面开展实验对比了几种优化策略的训练效果：

训练策略 Accuracy （Train/Valid/Test）
Gradient Descent 95.3% / 95.4% / 95.0%
Momentum 97.1% / 96.4% / 96.4%
Adagrad 96.7% / 96.4% / 96.0%
Adam 97.5% / 96.8% / 96.7%

各accuracy指标的变化曲线如下图所示：

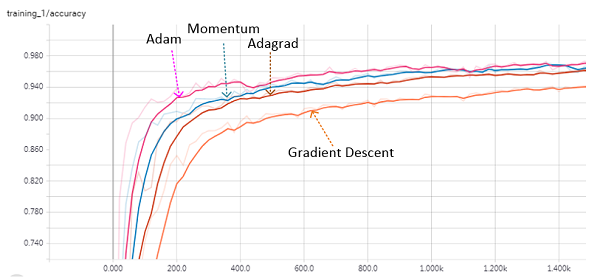
acc_compare_scheme

可以看出，优化策略调整之后，accuracy上升趋势提早（收敛加快），这说明达到相同的指标，新策略比旧策略所需的训练迭代次数更少，这对于提高深度学习训练效率具有极其重要的意义。接下来，在Adam的基础上，进一步调整learning_rate，num_epochs等超参数，经过一定时间的学习（≈10min），得出最终的预测结果为：

train accuracy: 0.9851
valid accuracy: 0.9684
test accuracy: 0.9679

2.3.2.正则化-Dropout

对上面的最后预测结果进行bias-variance分析，假设bayes_optimal=human_level=0.99，则：

avoidable bais --> 1 - train accuracy = 0.005
variance --> train accuracy - valid accuracy = 0.017

于是，要进一步改进模型效果，需要从Variance入手，解决所出现的轻微Overfitting。这里拟采用Dropout来进行模型优化。Dropout机制下，每次所训练的神经网络会以一定概率去掉一些节点，其示意图如下（参考原文献）：

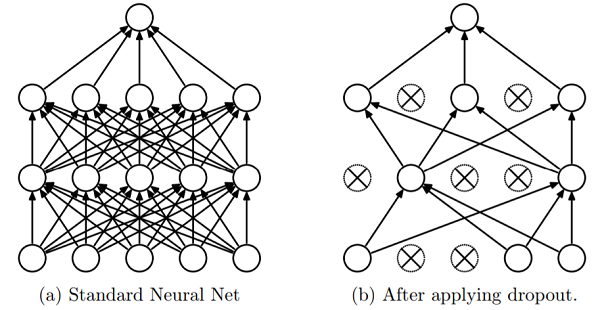
dropout_graph

由Dropout所产生的效用可形象地概括为以下两点：

  • 每一次训练时，去掉一些节点，相当于实现了shrink weight，平抑了噪声，产生“正则化”效果，减少过拟合。
  • 节点依概率随机去除，使得多次训练间的模型存在差异，产生“集成学习”的效果，提高整体精度。

这里采用tf.nn.dropout()函数实现针对于隐层的Dropout，经过较长时间的训练（≈20min），得出最终的结果为：

train accuracy: 0.997
valid accuracy: 0.968
test accuracy: 0.969

实验结果看来，经过更长时间的训练，MLP训练精度已经达到99.7%，这是一个很不错的结果，而测试精度徘徊于97%左右，要做进一步提升或还需从其他改进策略入手。

3.实验小结

本文通过搭建多层全连接神经网络（MLP），开展了MNIST分类实验。在该实验中，我们对比了不同优化策略（GD、Adam等）对于训练过程快慢的影响，尝试了Dropout策略以应对过拟合问题。任务最终取得了不错的效果。

此外我们还注意到，为达到较高的精度，MLP需要较长的时间训练，初步猜想其原因之一为所需训练的参数量大而导致的单次迭代计算耗时较长，这是由于MLP全连接模式所导致的。此外，过量的参数也容易引起过拟合现象。接下来，我们将进一步考察其他神经网络架构（如CNN）在当前任务背景下的应用，并与MLP进行对比分析。

4.参考资料